Learning forecasts of rare stratospheric transitions from short simulations

Please see our new paper adopting a novel prediction framework from computational chemistry to forecast extreme meteorological events, just submitted to Monthly Weather Review. The paper, led by Justin Finkel, presents a proof of concept study using a stochastically forced version of the classic Holton and Mass (1976) model of Sudden Stratospheric Warming events. We establish the “committor”, which provides the ideal combination of variables for predicting SSWs (where an SSW is a transition between the two fixed points in the Holton-Mass model). We also establish a method to compute it from relatively short integrations, i.e., integrations that are short relative to the time scale of the event, and much shorter than the return time scale of events.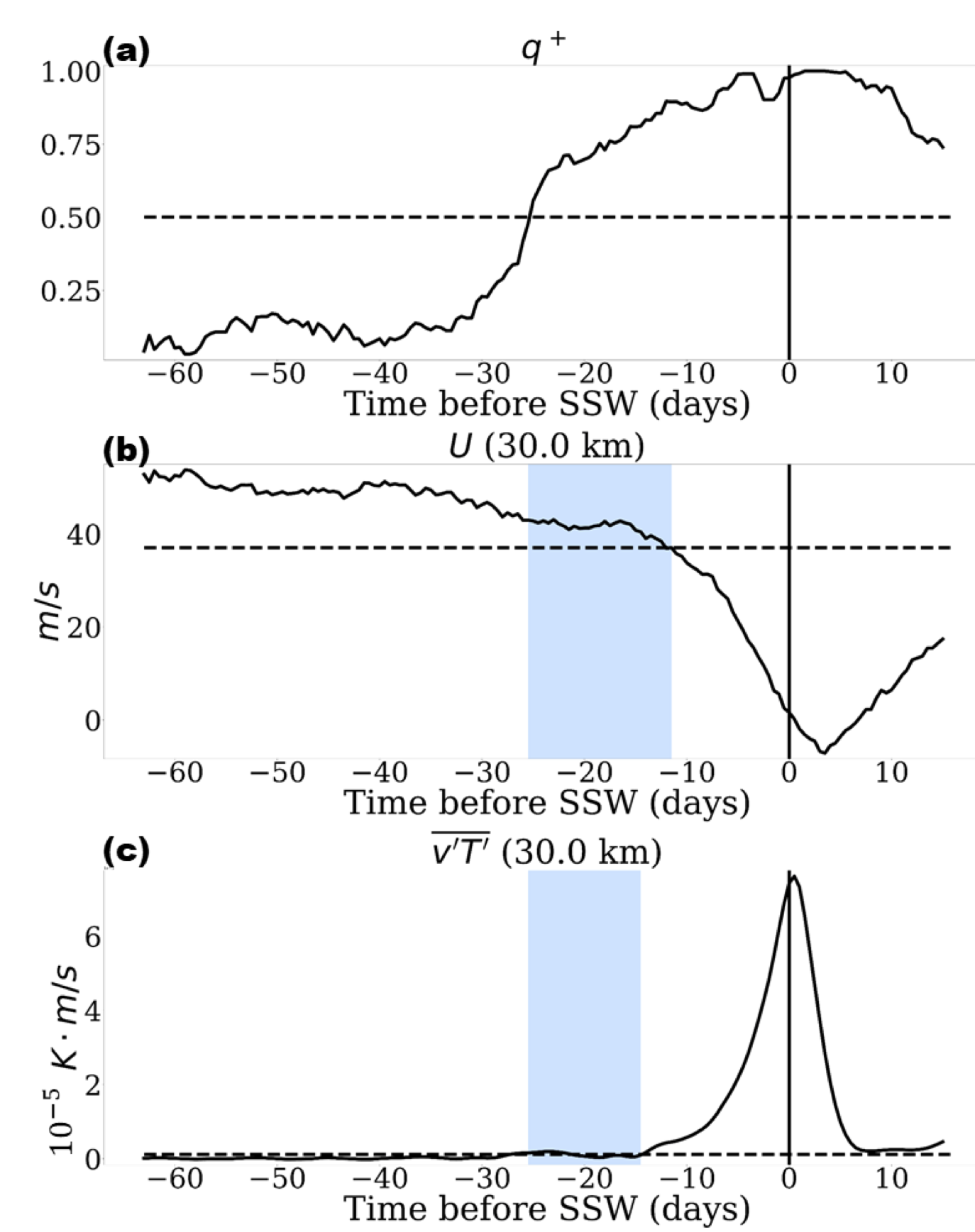

Justin Finkel is a graduate student at the University of Chicago, working with my colleague at the Courant, Jonathon Weare. Other coauthors include Robert Webber (also at the Courant) and Dorian Abbot at Chicago.

For a bit more detail, here’s the abstract. Or you can check out the paper directly!

Nonlinear atmospheric dynamics produce rare events that are hard to predict and attribute due to many interacting degrees of freedom. A sudden stratospheric warming event is a model example. Approximately once every other year, the winter polar vortex in the boreal stratosphere rapidly breaks down, inducing a shift in midlatitude surface weather patterns persisting for up to 2-3 months. In principle, lengthy numerical simulations can be used to predict and understand these rare transitions. For complex models, however, the cost of the direct numerical simulation approach is often prohibitive. We describe an alternative approach which only requires relatively short-duration computer simulations of the system. The methodology is illustrated by applying it to a prototype model of an SSW event developed by Holton and Mass (1976) and driven with stochastic forcing. While highly idealized, the model captures the essential nonlinear dynamics of SSWs and exhibits the key forecasting challenge: the dramatic separation in timescales between the dynamics of a single event and the return time between successive events. We compute optimal forecasts of sudden warming events and quantify the limits of predictability. Statistical analysis relates these optimal forecasts to a small number of interpretable physical variables. Remarkably, we are able to estimate these quantities using a data set of simulations much shorter than the timescale of the warming event. This methodology is designed to take full advantage of the high-dimensional data from models and observations, and can be employed to find detailed predictors of many complex rare events arising in climate dynamics.