See the forest and the trees!
Published:
Congratulations to Dave Connelly, who just submitted his first paper! It is about the use of regression forest to represent atmospheric gravity wave momentum transport to JAMES! The manuscript makes two important steps forward. First, it shows that a “boosted forest” approach, where you train each subsequent decision tree on the residual (as sketched below), can out perform a “random forest” where you combine a number of decision trees, averaging the result. This was well known in the ML community, but less so in the climate sciences. Second, Dave found that techniques from interpretable AI could be used to improve the training of a data driven parameterization. Using feature importance metrics, he found that his origional boosted forest wasn’t using enough information about latitude. By forcing the method to predict the latitude as well, he could build trees that incorporate this information more effectively!
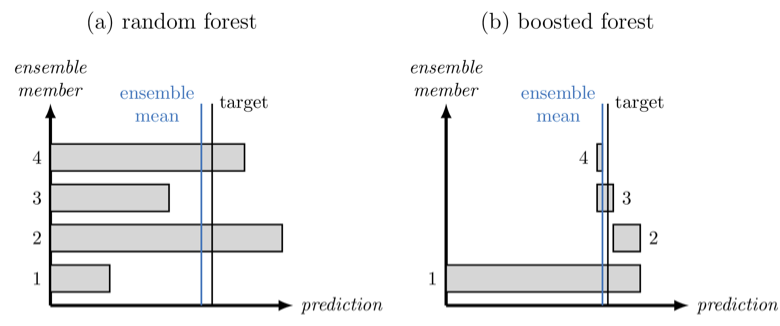
Dave’s plain language summary does a nice job of explaining the big picture. Parameterizations are reduced-complexity models that estimate the effects of physical processes smaller than what can be resolved by the grid of a weather or climate model. While necessary for realistic simulations, they are a source of uncertainty in climate projections. Recently, machine learning has been used to augment or replace conventional parameterizations of atmospheric gravity waves, a type of motion by which disturbances near the Earth’s surface can affect the wind higher up. We compare several machine learning approaches to the gravity wave parameterization problem. In particular, we test neural networks against random and boosted forests, which are built around flowchart-like models called regression trees. We find that boosted forests, though not widely used for climate model parameterization, are especially successful, scoring as well as or better than neural networks on various performance metrics. We then provide proof-of-concept of a novel method to retrain the boosted forest so that it uses its input data more in line with the physics of the system, and show that this technique improves the forest’s behavior when used together with an atmospheric model.